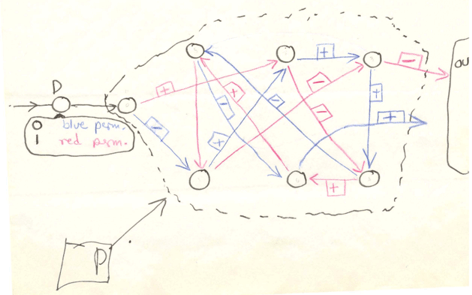
Машина НэшаАгентство национальной безопасности США (National Security Agency, NSA) в феврале 2012 года опубликовало два письма известного математика, лауреата нобелевской премии по экономике, героя голливудского фильма "Игры разума" Джона Нэша. Письма датированы 1955 годом. Нэш пишет, что является специалистом по теории игр, интересуется криптографией и хотел бы поделиться с NSA идеями построения надежных шифровальных машин. Напомним, что аббревиатуру NSA до недавнего времени шутливо расшифровывали как No Such Agency – Нет Такого Агентства – настолько секретной была эта организация. Не удивительно, что Нэш посылает письмо не напрямую, а через посредника – американский исследовательский центр RAND, который по сведениям знакомых Нэшу математиков сотрудничает с NSA. Как известно, Клод Шеннон считал, что совершенная криптосистема должна противостоять атакам противника, который знает статистические свойства открытых текстов, перехватывает шифртексты и обладает неограниченными вычислительными возможностями по их анализу. Нэш считает по-другому. Противник знает и шифртексты и открытые тексты и вообще знает все, кроме ключа, но его вычислительные ресурсы ограничены. Для защиты от подобного противника шифрование должно быть организовано так, что с увеличением длины ключа сложность его определения растет с экспоненциальной скоростью. Нэш выдвигает «экспоненциальную гипотезу» (exponential conjecture): для всех достаточно сложных преобразований зашифрования сложность определения ключа – экспоненциальная. Другими словами, почти все шифровальные машины надежны (unbreakable). Нэш обращает внимание, что «поскольку правительство США не желает, чтобы другие государства использовали криптосистемы, которые мы не сможем атаковать, желательно держать данный общий принцип (экспоненциальную гипотезу) в секрете». Во втором письме Нэш описывает примерное строение unbreakable машины. У машины Нэша есть внутреннее состояние S – двоичный n-вектор. На тактах работы машина изменяет это состояние и преобразует очередной бит открытого текста x в очередной бит шифртекста y. Такт работы описывается следующим образом: S ← FK(S, y), y ← x + fK(S, y). Здесь K – ключ, FK – функция переходов между состояниями, fK – функция выхода (со значениями 0 и 1), сложение битов выполняется по модулю 2. Нэш не уточняет, как выбирать начальные значения S и y. Можно считать, что начальные значения либо являются частью ключа, либо фиксированы. Нэш предлагает строить FK на основе двух преобразований – синего, которое применяется при y = 0, и красного, которое применяется при y = 1. Описание этих преобразований и является ключом K. На следующем чертеже из письма Нэша биты состояния обведены пунктирной линией, бит y подается слева. Синие и красные стрелки описывают перестановки битов состояния в зависимости от y. Знак «–» над стрелкой означает, что при перестановке бит дополнительно инвертируется, знак «+» означает отсутствие инверсии. Если занумеровать биты состояния слева направо и сверху вниз от S1 до S7, то синее преобразование меняет (S1, S2, S3, S4, S5, S6, S7, y) на (y, S7 + 1, S5, S3, S1 + 1, S2 + 1, S4), красное преобразование меняет тот же вектор на (y, S6, S1, S5 + 1, S2 + с, S7 + 1, S3 + 1). Здесь c – неопределенный бит, поскольку Нэш не поставил знак +/– над одной из красных стрелок. Чертеж дополнительно определяет функцию выхода: fK(S, 0) = S6, fK(S, 1) = S4 + 1. Машина Нэша была отвергнута специалистами NSA со следующей формулировкой: «Система, которую Вы описали, была тщательно проанализирована на предмет использования в военных или других государственных целях. Было установлено, что криптографические решения, использованные в Вашей системе, интересны, но не удовлетворяют действующим требованиям безопасности…. Сожалеем, что не можем дать более подробный ответ». Продолжение следует... |
Новости
26.02.2026
План семинара весна 2026
05.02.2026
Сотрудничество с ОИПИ НАН Беларуси
30.12.2025
О награждении Ю.С. Харина
15.10.2025
25 лет НИИ ППМИ
17.06.2025
Digital Expo 2025
16.05.2025
XХX научно-практическая конференция
19.12.2024
Выборы Президента Республики Беларусь
12.12.2024
Награждение победителей конкурса
10.12.2024
Визит Министра образования
|